Asal Sayılar Konu Anlatımı ve Testleri
Asal sayılar, matematikte temel bir kavram olup, birçok teorik ve pratik uygulamada önemli bir rol oynamaktadır. Bu yazıda asal sayıların tanımı, özellikleri, tarihçesi ve belirlenmesi için kullanılan test yöntemleri detaylandırılmaktadır. Asal sayıların matematiksel ve kriptografik önemi de vurgulanmaktadır.
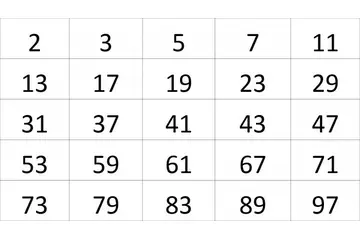
Asal Sayılar Konu Anlatımı Ve Testleri Asal sayılar, matematikte önemli bir yere sahip olan ve birçok teorik ve pratik uygulamada karşımıza çıkan sayılardır. Bu makalede asal sayıların tanımı, özellikleri, asal sayıların tarihçesi ve çeşitli test yöntemleri detaylı bir şekilde ele alınacaktır. Asal Sayının Tanımı Asal sayılar, sadece 1 ve kendisi olmak üzere tam iki pozitif böleni olan doğal sayılardır. Örneğin, 2, 3, 5, 7, 11 gibi sayılar asal sayılardır. Ancak 1, asal sayı olarak kabul edilmemektedir. Asal sayılar, matematiksel analiz, sayı teorisi ve kriptografi gibi birçok alanda temel yapı taşlarıdır. Asal Sayıların Özellikleri Asal sayıların bazı temel özellikleri şunlardır:
Asal Sayıların Tarihçesi Asal sayılar, tarih boyunca matematikçiler tarafından incelenmiş ve birçok ilginç teori ve sonuç geliştirilmiştir. Antik Yunan'da, matematikçi Eratosthenes, asal sayıları bulmak için bir yöntem geliştirmiştir. Bu yöntem, “Eratosthenes süzgeci” olarak bilinir ve asal sayıları belirlemede etkili bir yöntemdir. Asal Sayıların Belirlenmesi İçin Test Yöntemleri Asal sayıları belirlemek için çeşitli test yöntemleri bulunmaktadır. Bu yöntemlerden bazıları şunlardır:
Asal Sayılar ve Kriptografi Asal sayılar, modern kriptografide önemli bir rol oynamaktadır. Özellikle RSA algoritması gibi şifreleme yöntemleri, büyük asal sayıların çarpanları üzerinde çalışmaktadır. Bu yöntem, bilgi güvenliğini sağlamak için kullanılmaktadır. Asal sayıların büyük olması, şifrelemenin güvenliğini artırmaktadır. Sonuç Asal sayılar, matematiğin temel taşlarından birini oluşturmakta ve birçok alanda uygulama bulmaktadır. Bu yazıda, asal sayıların tanımı, özellikleri, tarihçesi ve belirlenmesi için kullanılan test yöntemleri detaylı bir şekilde ele alınmıştır. Asal sayılar üzerine yapılan araştırmalar, matematiksel teorilerin gelişimine katkı sağlamakta ve bilgi güvenliği gibi pratik alanlarda önemli bir rol oynamaktadır. Ekstra Bilgiler Bu makalede asal sayılar hakkında geniş bir bilgi sunulmuş olup, bu temel kavramların matematik ve diğer alanlar üzerindeki etkisi vurgulanmıştır. Asal sayılar üzerine yapılacak daha fazla araştırma, matematiksel bilginin derinleşmesine ve farklı disiplinlerde uygulanmasına olanak tanıyacaktır. |












Asal sayılar hakkında yazdıklarınız oldukça bilgilendirici. Asal sayının tanımı ve özellikleri gerçekten çok önemli konular. Özellikle Eratosthenes Süzgeci yöntemi ile asal sayıları bulmanın ne kadar etkili olduğunu belirtmeniz, bu konuda bilgi edinmek isteyenler için oldukça faydalı. Ayrıca, 1 sayısının asal sayılar arasında yer almadığını vurgulamanız da çok kritik bir nokta. Asal sayıların sayılar teorisindeki yerini anlamak, matematik çalışmalarında büyük bir avantaj sağlıyor. Peki, asal sayıların günlük hayattaki uygulamaları nelerdir?
Abdünnasır, yorumunuz için teşekkür ederim. Asal sayılar matematiğin temel taşlarından biridir ve birçok alanda önemli uygulamalara sahiptir.
Günlük Hayattaki Uygulamaları: Asal sayılar, özellikle kriptografi alanında büyük bir rol oynar. İnternet güvenliği sağlamak için kullanılan birçok şifreleme algoritmasında asal sayılardan yararlanılır. Örneğin, RSA şifrelemesi, iki büyük asal sayının çarpımı ile oluşturulan bir anahtara dayanır. Bu sayede, verilerin güvenli bir şekilde iletilmesi sağlanır.
Ayrıca, asal sayılar, bilgisayar bilimlerinde ve algoritmalarda da sıkça kullanılmaktadır. Veri yapıları ve algoritmaların performansını artırmak için asal sayılarla ilgili teknikler geliştirilmiştir. Örneğin, hash tablolarında çarpan olarak asal sayılar kullanmak, çarpışma olasılığını azaltır ve verimliliği artırır.
Sonuç olarak, asal sayılar sadece matematiksel bir kavram olmanın ötesinde, teknoloji ve güvenlik alanında da kritik bir öneme sahiptir. Bu nedenle, asal sayılar ve özellikleri üzerine yapılan çalışmalar, yalnızca teorik değil, pratik açıdan da oldukça değerlidir.