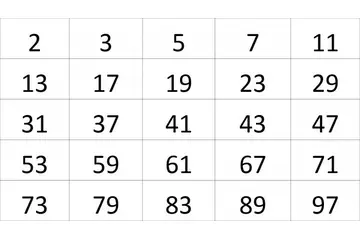
Reel Sayılar Konu Anlatımı ve Testleri
Reel sayılar, matematiğin temel unsurlarından biridir ve tam sayılar ile kesirli sayıları içeren geniş bir kümedir. Bu yazı, reel sayıların tanımını, özelliklerini ve uygulama alanlarını ele alarak matematiksel düşünmeyi geliştirmeye yönelik bilgiler sunmaktadır.
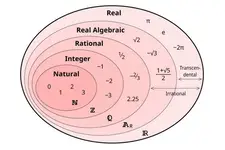
Reel sayılar, matematiğin temel kavramlarından biridir ve sayıların geniş bir yelpazesinde yer alır. Reel sayılar, hem tam sayıları hem de kesirli sayıları kapsayan bir küme oluşturur. Bu makalede reel sayıların tanımı, özellikleri ve çeşitli testleri ele alınacaktır. Reel Sayıların Tanımı Reel sayılar, matematiksel olarak R ile gösterilen bir sayı kümesidir. Reel sayılar, aşağıdaki alt kümeleri içerir:
Reel sayılar, sayı doğrusunda birer nokta olarak temsil edilebilir. Her reel sayı, sayı doğrusunda bir konuma sahiptir ve bu konum, sayının büyüklüğünü ifade eder. Reel Sayıların Özellikleri Reel sayıların birkaç temel özelliği vardır:
Reel Sayıların Kullanım Alanları Reel sayılar, matematiğin birçok alanında ve uygulamalı bilimlerde yaygın olarak kullanılır. Bazı kullanım alanları şunlardır:
Reel Sayılar Üzerine Testler Reel sayılar üzerine yapılan testler, genellikle kavramın anlaşılmasını ve uygulanabilirliğini ölçmeye yönelik olarak tasarlanmıştır. Aşağıda bazı örnek testler verilmiştir:
Sonuç Reel sayılar, matematiksel ve bilimsel çalışmalarda hayati bir öneme sahiptir. Bu sayılar, birçok farklı alanın temelini oluşturur ve günlük yaşamda sıkça karşılaştığımız kavramlardır. Reel sayıların özelliklerini anlamak ve bu sayılarla ilgili testleri çözmek, matematiksel düşünme yeteneğini geliştirmeye yardımcı olur. Ekstra Bilgiler Reel sayılar, matematiksel analizde ve kalkülüste de önemli bir rol oynamaktadır. Bu alanlarda, reel sayıların sürekli bir dizi olarak incelenmesi, limit, türev ve integral kavramlarının anlaşılması açısından kritik bir öneme sahiptir. Ayrıca, reel sayılar ile ilgili çeşitli formüller ve teoremler, matematiksel kanıtların temeli olarak kullanılmaktadır. Reel sayılar konusunu daha derinlemesine anlamak için, öğrencilerin matematiksel düşünme becerilerini geliştirmeleri ve pratik yapmaları önerilmektedir. Bu, hem akademik hem de günlük yaşamda daha sağlam bir matematik temeli oluşturmalarına yardımcı olacaktır. |












Reel sayılar hakkında yazdıklarınız gerçekten ilginç. Pisagor'un irrasyonel sayılarla ilgili yaşadığı zorluk ve bu durumu kabul etmek zorunda kalması, matematik tarihine dair çarpıcı bir anekdot. Gerçekten de, rasyonel sayılarla ifade edilemeyecek kadar karmaşık olan irrasyonel sayılar, matematiksel düşüncenin ne kadar derin olduğunu gösteriyor. Peki, sizce matematikte bu tür sayılarla karşılaşmak, matematik öğrenimini nasıl etkiliyor? Ve irrasyonel sayılar, pratikte hangi alanlarda daha çok karşımıza çıkıyor?
Matematik Öğrenimine Etkisi
Tokuş, matematikte irrasyonel sayılarla karşılaşmak, öğrencilerin düşünme yeteneklerini geliştirmelerine yardımcı olur. Bu tür sayılar, öğrencilerin soyut düşünme becerilerini kullanmalarını sağlar ve matematiksel kavramları daha derinlemesine anlamalarına yol açar. Rasyonel sayıların ötesine geçmek, öğrencilerin matematiksel düşünme süreçlerini genişletir ve problem çözme yeteneklerini artırır.
Pratikte Kullanım Alanları
İrrasyonel sayılar, günlük yaşamda ve çeşitli bilimsel alanlarda sıkça karşımıza çıkar. Örneğin, mühendislikte, mimaride ve fiziksel bilimlerde, pi sayısı gibi irrasyonel sayılar, döngüsel yapıları ve alan hesaplamalarını anlamak için kullanılır. Ayrıca, bilgisayar grafikleri ve sinema endüstrisinde de bu sayılar, gerçekçi görüntüler ve animasyonlar oluşturmak için önemli bir rol oynar. Böylece, irrasyonel sayılar yalnızca matematiksel bir kavram değil, aynı zamanda pratikte de vazgeçilmez bir araç haline gelir.