Rasyonel Sayılar Konu Anlatımı ve Testleri
Rasyonel sayılar, pay ve paydadan oluşan kesir biçiminde ifade edilebilen tam sayılar grubudur. Matematiksel işlemlerde önemli bir yere sahip olan bu sayılar, temel özellikleri ve örnekleri ile birlikte incelenir. Makalede, rasyonel sayıların tanımı, özellikleri, matematiksel işlemleri ve test örnekleri ele alınmaktadır.
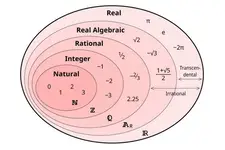
Rasyonel sayılar, matematiksel bir kavram olarak, tam sayılar arasında belirli bir orantı ve yapı sunan sayı grubunu ifade eder. Rasyonel sayılar, pay ve paydadan oluşan kesir biçiminde yazılabilen sayılardır. Bu makalede, rasyonel sayıların tanımı, özellikleri, örnekleri ve testleri üzerinde durulacaktır. Rasyonel Sayıların Tanımı Rasyonel sayılar, genel olarak a/b biçiminde ifade edilen, burada 'a' tam sayı ve 'b' sıfırdan farklı bir tam sayı olmak üzere tanımlanır. Bu durumda, 'a' sayısı kesirin payını, 'b' sayısı ise paydasını temsil eder. Rasyonel sayılar, pozitif, negatif ve sıfır değerlerini alabilir. Rasyonel Sayıların Özellikleri Rasyonel sayıların çeşitli özellikleri bulunmaktadır. Bu özellikler, rasyonel sayıların matematiksel işlemlerine ve genel kullanımına yön vermektedir.
Rasyonel Sayıların Örnekleri Rasyonel sayılara örnek vermek gerekirse;
Rasyonel Sayılar ile İlgili Matematiksel İşlemler Rasyonel sayılar üzerinde yapılan temel matematiksel işlemler şunlardır:
Rasyonel Sayılarla İlgili Testler Rasyonel sayılar konusunda becerilerinizi ölçmek için çeşitli testler uygulamak faydalı olabilir. Aşağıda bazı örnek test soruları verilmiştir: 1. Aşağıdaki ifadelerden hangisi bir rasyonel sayı değildir? a) 1/3 b) 0 c) √2 d) -4/52. 3/4 + 1/2 işleminin sonucu nedir?3. -5/6 - 1/3 işleminin sonucu nedir?4. 2/3 × 3/5 işleminin sonucu nedir?5. 4/5 ÷ 2/3 işleminin sonucu nedir? Sonuç Rasyonel sayılar, matematikte önemli bir yere sahip olup, birçok farklı alanda karşımıza çıkmaktadır. Tanımları, özellikleri ve matematiksel işlemlerinin yanı sıra, rasyonel sayılarla ilgili testler yaparak bu konudaki bilgimizi pekiştirmek mümkündür. Rasyonel sayılar, matematiksel düşünme becerilerini geliştirmek ve daha karmaşık matematiksel kavramları anlamak için temel bir yapı sunar. |












Rasyonel sayılarla ilgili bilgiler oldukça kapsamlı görünüyor. Özellikle toplama ve çıkarma işlemlerinin nasıl yapıldığını açıklamanız çok faydalı. Peki, paydaları eşitlemenin zorluğuyla karşılaştığınızda ne gibi yöntemler kullanıyorsunuz? Bu tür işlemlerde pratikte sıkça karşılaşılan hatalar neler? Rasyonel sayılar arasında işlem yaparken, özellikle de paydaları eşitleme sürecinde dikkat edilmesi gereken noktaları paylaşmanız ilginç olabilir.
Paydaları Eşitleme Yöntemleri
Rasyonel sayılarla işlemler yaparken, paydaları eşitlemek için birkaç farklı yöntem kullanabilirsiniz. Öncelikle, en küçük ortak payda (EKP) bulmak en yaygın yöntemdir. İki veya daha fazla paydanın çarpanlarını belirleyip, bu çarpanların en küçük ortak katını bulduktan sonra, her bir rasyonel sayıyı bu ortak paydaya göre dönüştürebilirsiniz. Ayrıca, paydaları doğrudan çarparak da eşitleme yapabilirsiniz, bu durumda her iki paydanın çarpımını ortak olarak kullanabilirsiniz.
Pratikte Karşılaşılan Hatalar
Paydaları eşitleme işlemi sırasında karşılaşılan yaygın hatalardan biri, en küçük ortak paydanın yanlış hesaplanmasıdır. Bu, sonuçta yanlış bir değerle işlem yapmanıza neden olabilir. Diğer bir hata ise, paydaları eşitleme işleminde her iki kesiri de düzgün bir şekilde dönüştürmemek; bir kesiri dönüştürürken diğerini unutmak sık karşılaşılan bir durumdur. Ayrıca, payda eşitlenirken payların da doğru bir şekilde çarpılmaması veya eklenmemesi, işlemin sonucunu etkileyebilir.
Dikkat Edilmesi Gereken Noktalar
Rasyonel sayılarla işlem yaparken dikkat edilmesi gereken en önemli nokta, paydaların sıfır olmaması gerektiğidir; çünkü sıfıra bölme matematiksel olarak tanımsızdır. Ayrıca, paydaları eşitleme işlemi sonrasında payların doğru bir şekilde hesaplandığından emin olmalısınız. İşlemin sonunda, elde edilen sonucu sadeleştirmek de önemlidir; böylece daha basit bir ifade elde edilebilir. Bu tür işlemlerde pratik yaparak ve farklı örnekler üzerinde çalışarak hatalarınızı minimize edebilirsiniz.